Wherever these notes use the float primitive type, they generally apply to double also.

The JVM uses the “round to nearest, ties to even” rounding rule for floating point values. From the JVM spec:

The round to nearest rounding policy applies to all floating-point instructions except for (i) conversion to an integer value and (ii) remainder. Under the round to nearest rounding policy, inexact results must be rounded to the representable value nearest to the infinitely precise result; if the two nearest representable values are equally near, then the value whose least significant bit is zero is chosen.

The round to nearest rounding policy corresponds to the default rounding-direction attribute for binary arithmetic in IEEE 754, roundTiesToEven.

As alluded to above, the policy is not the same for values converted to integers, where “round towards zero” is used instead.

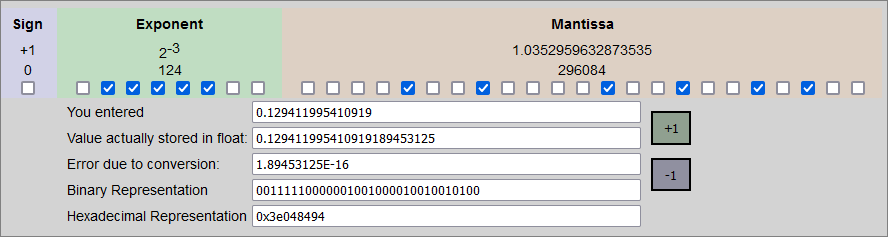
Example: raw data value 0.129411995410919

Using this online float converter, here is an example:

In Java, to convert the data value to hex:

1

Integer.toHexString(Float.floatToRawIntBits(0.129411995410919f)); // 3e048494

To reverse the above process:

1
2
3

byte[] datax = HexFormat.of().parseHex("3e048494");
ByteBuffer buffer = ByteBuffer.wrap(datax);
System.out.println(buffer.getFloat());

The above is big-endian. If you happen to have little-endian hex (or bytes), then use the following:

1
2
3

byte[] datax = HexFormat.of().parseHex("9484043e");
ByteBuffer buffer = ByteBuffer.wrap(datax).order(ByteOrder.LITTLE_ENDIAN);
System.out.println(buffer.getFloat());

The above conversions from hex to float only give us the following number:

0.129412

What happened to all that extra precision we started with?

The screenshot from the online conversion tool shows us that the actual number stored by 0x3e048494 is:

0.129411995410919189453125

Using that tool’s +1 and -1 buttons we can see what the next and previous values are:

0x3e048493 -> 0.12941198050975799560546875
0x3e048494 -> 0.129411995410919189453125
0x3e048495 -> 0.12941201031208038330078125

Each of these “actually stored” decimal values has a related Java “display” value, which is much shorter than these numbers.

The static Float.toString() method handles this (explicitly or implicitly):

1
2
3

Float.toString(0.12941198050975799560546875f); // 0.12941198
Float.toString(0.129411995410919189453125f);   // 0.129412
Float.toString(0.12941201031208038330078125f); // 0.12941201

The rules for string length:

There must be at least one digit to represent the fractional part, and beyond that as many, but only as many, more digits as are needed to uniquely distinguish the argument value from adjacent values of type float.

You can see that the lengths of the displayed numbers are as long as they need to be to distinguish each from the others.

If you want to retrieve the full stored value in a float, you can use a BigDecimal constructor:

1

BigDecimal bd = new BigDecimal(0.129411995410919f);

The above bd contains 0.129411995410919189453125.

This conversion is a bit pointless - you have already incurred the loss of accuracy.

Note - if you use the following:

1

BigDecimal bd = BigDecimal.valueOf(0.129411995410919f);

Then you get 0.12941201031208038 - which is a new number we have not seen before!

This is because valueOf() takes a double:

Translates a double into a BigDecimal, using the double’s canonical string representation provided by the Double.toString(double) method.

So our float raw data is actually handled as a double (with more precision - but still a loss of accuracy). In the above example, we used the double rules for converting to a display string.

If accuracy is important to you, you are better off using nothing but BigDecimals from the start:

1

BigDecimal bd = new BigDecimal("0.129411995410919");

This has no loss of accuracy, because it does not involve any conversion from float (or from double). This numeric value exactly represents the provided String as a decimal number.